Далее представлен краткий конспект разбора алгоритма быстрой сортировки по книге «Алгоритмы. Построение и анализ» (Томас Кормен, Чарльз Лейзерсон, Рональд Ривест, Клиффорд Штайн). Примеры кода написаны на языке Java.

Время работы

• Наихудший вариант: O(n^2)
• В среднем случае: O(n*logn)

Свойства:

• Не требует дополнительной памяти, работает с тем же массивом данных. Использует принцип “разделяй и властвуй”. В большинстве случаев работает за время O(n* logn) и является одним из самых эффективных методов сортировки.

Принцип работы:

1. Выбирается опорный элемент (рандомно, либо последний/первый элемент в массиве, либо среднее арифметическое, если массив состоит из чисел)
2. Массив разбивается на два подмассива, в одном элементы не больше опорного, в другом не меньше опорного
3. Полученные подмассивы сортируются рекурсивно вызовом процедуры быстрой сортировки

Метод быстрой сортировки:

1
2
3
4
5
6
7
8
9
10
11
12
13

    /**
     * 
     * @param a[] - входящий массив
     * @param l - индекс крайне левого элемента, с которого начать сравнивания
     * @param r  - индекс крайне правого элемента, с которого начать сравнивания
     */
    public void quickSort(int[] a, int l, int r) {
        if (l < r) {
            int q = partition(a, l, r);
            quickSort(a, l, q);
            quickSort(a, q + 1, r);
        }
    }

Для запуска сортировки необходимо выполнить: quickSort(array, 0, array.length - 1);

Метод разбиения массива

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

 private int partition(int[] a, int l, int r) {

        int x = l; // метка на следующий элемент после меньшей части опорного
        int pivot = a[r]; //опорный элемент, относительно которого идут сравнения
        for ( int i = l; i <= r; i++ ) // цикл от начального до конечного
        {
            if ( a[i] <= pivot )
            {
                // если текущий элемент меньше опроного, то меняем местами текущий элемент
                // и элемент на который указывает метка следующего элемента за меньшими опроными
                swap(a, i, x);
                x++; // увеличиваем метку, т.к. до этой метки остались только элементы меньшие опроному
            }
        }
        return --x;
    }

Пример работы из книги Кормена:

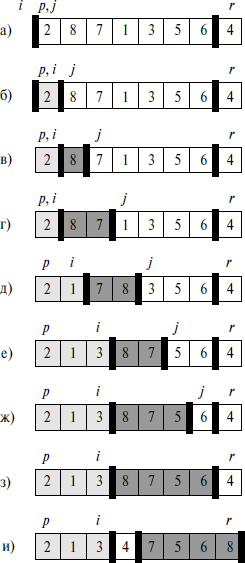
Небольшое отличие: в коде x - здесь можно считать i + 1, а счетчик i в коде здесь - это j

Пример разделения массива в середине работы процедуры partition: